Naive Bayes algorithm
A Simple and Effective Approach for Classification Tasks.
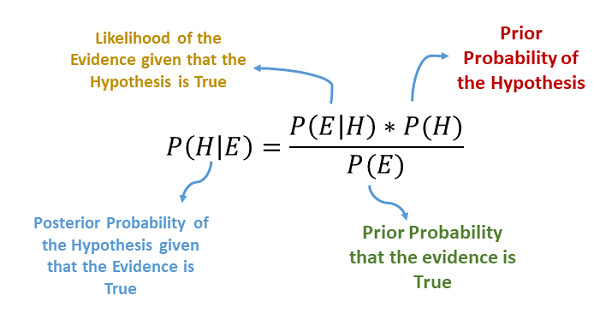
Naive Bayes is a machine learning algorithm that is used for classification tasks. It is based on the idea of applying Bayes’ theorem, which describes the probability of an event based on prior knowledge of conditions that might be related to the event.
The algorithm makes the assumption that all of the features in the dataset are independent of each other, which is why it is called “naive.” This means that the presence or absence of one feature does not affect the probability of the other features.
To classify a new data point, the algorithm first calculates the probability of the new data point belonging to each class. It then chooses the class with the highest probability as the predicted class for the new data point.
To calculate the probability of a new data point belonging to a given class, the algorithm uses Bayes’ theorem, which states that the probability of A given B is equal to the probability of B given A times the probability of A, divided by the probability of B.
For example, suppose we have a dataset with two classes: “spam” and “not spam.” We can use Bayes’ theorem to calculate the probability that a new email belongs to the “spam” class, given that it contains the word “Viagra.” We first need to calculate the probability of the word “Viagra” appearing in a “spam” email, and the probability of the word “Viagra” appearing in a “not spam” email. We then multiply these probabilities by the overall probability of the email belonging to the “spam” class, and divide by the probability of the word “Viagra” appearing in any email.
Once we have calculated the probabilities for each class, we choose the class with the highest probability as the predicted class for the new data point.
Naive Bayes is a simple and effective algorithm for classification tasks, and it can be used with a variety of different types of data. It is particularly well-suited for text data, where it can be used to classify documents according to their content. It is also often used in spam filtering and other applications where the goal is to identify specific types of data.
Conditional probability
Bayes’ theorem is a mathematical formula used in probability and statistics to calculate the conditional probability of an event. It is named after Thomas Bayes, an 18th-century mathematician and minister who developed the formula in his work on the theory of probability.
The formula for Bayes’ theorem is:
P(A|B) = (P(B|A) * P(A)) / P(B)
where:
- P(A|B) is the conditional probability of event A, given that event B has occurred
- P(B|A) is the conditional probability of event B, given that event A has occurred
- P(A) is the probability of event A occurring
- P(B) is the probability of event B occurring
In simple terms, Bayes’ theorem allows us to calculate the probability of an event occurring, given that another event has occurred. It does this by using the probabilities of the two events occurring independently, and combining them to give the probability of the events occurring together.
For example, suppose we have a medical test for a certain disease, and we want to calculate the probability that a patient has the disease, given that the test result is positive. Using Bayes’ theorem, we would first need to know the probability of a positive test result for patients with the disease (P(B|A)), the probability of a positive test result for patients without the disease (P(B|not A)), the overall probability of the disease occurring (P(A)), and the overall probability of a positive test result (P(B)).
We can then plug these values into Bayes’ theorem to calculate the probability that a patient has the disease, given a positive test result:
P(A|B) = (P(B|A) * P(A)) / P(B)
For example, if the probability of a positive test result for patients with the disease is 90%, the probability of a positive test result for patients without the disease is 5%, the overall probability of the disease occurring is 1%, and the overall probability of a positive test result is 6%, we would calculate the probability as follows:
P(A|B) = (0.9 * 0.01) / 0.06 = 0.15
This means that the probability that a patient has the disease, given a positive test result, is 15%.
In summary, Bayes’ theorem is a formula used in probability and statistics to calculate the conditional probability of an event. It uses the probabilities of the two events occurring independently to calculate the probability of the events occurring together, and it can be useful for a variety of applications, such as medical testing or predictive modeling.
Independent vs Mutually exclusive events
Bayes’ theorem is a mathematical formula used to calculate the conditional probability of an event, given that another event has occurred. In order to use Bayes’ theorem, it is important to understand the difference between independent and mutually exclusive events.
Independent events are events that do not affect each other. For example, if we flip a coin, the outcome of the first flip does not affect the outcome of the second flip. The probability of the two flips being heads is the product of the probability of the first flip being heads and the probability of the second flip being heads.
Mutually exclusive events, on the other hand, are events that cannot occur at the same time. For example, if we flip a coin, the outcome cannot be both heads and tails at the same time. The probability of the two flips being heads or tails is the sum of the probability of the first flip being heads and the probability of the second flip being tails.
In Bayes’ theorem, the events A and B are independent if the probability of event A occurring does not affect the probability of event B occurring. This means that the probability of events A and B occurring together is the product of the probability of event A occurring and the probability of event B occurring.
On the other hand, events A and B are mutually exclusive if the probability of event A occurring is zero if event B occurs, and vice versa. This means that the probability of events A and B occurring together is the sum of the probability of event A occurring and the probability of event B occurring.
In summary, Bayes’ theorem is a formula used to calculate the conditional probability of an event, given that another event has occurred. It is important to understand the difference between independent and mutually exclusive events, because the formula uses different calculations depending on whether the events are independent or mutually exclusive.
Toy example: Train and test stages
To explain the naive Bayes algorithm using a toy example, let’s suppose we have a dataset with two classes: “red” and “blue.” We want to train a naive Bayes classifier to predict the class of a new data point based on two features: the shape of the object (either “round” or “square”) and its color (either “red” or “blue”).
The first step in training the classifier is to calculate the probabilities of each class in the dataset. In this example, let’s suppose that 60% of the objects in the dataset are “red” and 40% are “blue.”
Next, we need to calculate the probabilities of each feature for each class. For example, we need to calculate the probability that an object is “round” given that it is “red,” and the probability that an object is “round” given that it is “blue.” In this example, let’s suppose that 50% of the “red” objects are “round” and 50% are “square,” and that 30% of the “blue” objects are “round” and 70% are “square.”
Once we have calculated these probabilities, we can use them to predict the class of a new data point. Suppose we encounter a new object that is “round” and “blue.” To predict its class, we first calculate the probability of it belonging to the “red” class using Bayes’ theorem. This involves multiplying the probability of the object being “round” given that it is “red” by the probability of the object being “blue” given that it is “red,” and then multiplying the result by the overall probability of the object being “red.”
We then repeat this process to calculate the probability of the object belonging to the “blue” class. This involves multiplying the probability of the object being “round” given that it is “blue” by the probability of the object being “blue” given that it is “blue,” and then multiplying the result by the overall probability of the object being “blue.”
Finally, we compare the probabilities of the object belonging to each class, and choose the class with the highest probability as the predicted class for the new data point. In this example, the probability of the object belonging to the “blue” class is higher, so the classifier would predict that the object is “blue.”
This is a simple example of how the naive Bayes algorithm can be used for classification. In a real-world dataset, there would be many more features and classes, and the probabilities would be calculated using the entire dataset, rather than just a few sample values. But the basic process of using Bayes’ theorem to calculate the probabilities and predict the class of a new data point would be the same.
Naive Bayes on Text data
Naive Bayes is a machine learning algorithm that is commonly used for classification tasks, particularly in the field of natural language processing. It is called “naive” because it makes a strong assumption about the independence of the features in the data, which is often not true in real-world datasets. Despite this limitation, the algorithm is often effective and efficient, especially for text data.
When using naive Bayes on text data, the algorithm first converts the text data into a numerical representation, known as a feature vector. This is typically done using a method called “bag of words,” which ignores the order and context of the words in the text, and instead counts the number of times each word appears. The resulting feature vector is a sparse matrix, with a row for each document (e.g., an email or a sentence) and a column for each word in the vocabulary.
Once the text data has been converted into a feature vector, the naive Bayes algorithm can be applied. It calculates the probability of each class (e.g., “spam” or “not spam”) for each document, based on the probabilities of the words in the document belonging to that class. The algorithm makes the assumption that the words in the document are independent, which allows it to simplify the calculations and make them more efficient.
The final step is to make predictions based on the calculated probabilities. The algorithm typically predicts the class with the highest probability for each document, but other strategies can be used as well, such as setting a probability threshold or using a weighted average of the probabilities.
In summary, naive Bayes is a machine learning algorithm that is commonly used for text classification tasks. It converts the text data into a numerical representation using a bag of words, and then calculates the probabilities of each class for each document, based on the probabilities of the words in the document belonging to that class. The algorithm makes predictions based on these probabilities, and it is often effective and efficient, especially for text data.
Laplace/Additive Smoothing
Laplace smoothing, also known as additive smoothing, is a technique used to smooth categorical data in a dataset. It is often used in conjunction with the naive Bayes algorithm, which is a popular machine learning algorithm for classification tasks.
The idea behind Laplace smoothing is to add a small value (called the “smoothing parameter”) to each count in the dataset, to prevent zero probabilities from occurring. This is important because the naive Bayes algorithm relies on probabilities, and a zero probability would cause the algorithm to make incorrect predictions.
To understand why Laplace smoothing is necessary, consider a dataset with two classes: “spam” and “not spam.” We want to train a naive Bayes classifier to predict the class of a new email, based on the words that appear in the email. If a particular word never appears in any of the “spam” emails in the dataset, the probability of that word appearing in a “spam” email would be zero, which would cause the classifier to make incorrect predictions.
To avoid this problem, we can use Laplace smoothing. This involves adding a small value (such as 0.1) to each count in the dataset. For example, if a particular word appears in 10 “spam” emails and 0 “not spam” emails, the probability of that word appearing in a “spam” email would be calculated as (10+0.1) / (10+0.1+0+0.1) = 0.95, rather than just 10 / 10 = 1. This ensures that all probabilities are non-zero, which allows the naive Bayes algorithm to make more accurate predictions.
In summary, Laplace smoothing is a technique used to smooth categorical data in a dataset, by adding a small value to each count. It is often used in conjunction with the naive Bayes algorithm, to prevent zero probabilities from occurring and improve the accuracy of the predictions.
Log-probabilities for numerical stability
Log-probabilities are a technique used to improve the numerical stability of the naive Bayes algorithm, which is a popular machine learning algorithm for classification tasks. The idea is to convert probabilities to logarithmic form, which allows the algorithm to avoid underflow and overflow errors that can arise when working with very small or very large numbers.
To understand why log-probabilities are necessary, consider the example of a naive Bayes classifier that is trained to predict the class of a new email, based on the words that appear in the email. In this case, the classifier needs to calculate the probability of each word appearing in a “spam” email, as well as the probability of each word appearing in a “not spam” email. If a particular word appears in a very large number of emails, the probability of that word appearing in a “spam” email (or a “not spam” email) could be very close to 1, which would cause the classifier to make incorrect predictions.
To avoid this problem, we can use log-probabilities. This involves converting the probabilities to logarithmic form, using the log function. For example, if the probability of a particular word appearing in a “spam” email is 0.95, the log-probability would be log(0.95) = -0.05. This allows the classifier to avoid underflow and overflow errors, and make more accurate predictions.
In summary, log-probabilities are a technique used to improve the numerical stability of the naive Bayes algorithm. They involve converting probabilities to logarithmic form, which allows the algorithm to avoid underflow and overflow errors and make more accurate predictions.
Bias and Variance tradeoff
The bias-variance tradeoff is a fundamental concept in machine learning, and it applies to the naive Bayes algorithm as well. In general, the bias-variance tradeoff describes the tradeoff between two types of error that can occur when training a machine learning model: bias and variance.
Bias error arises when the model makes assumptions that are too simplistic or inflexible, and as a result, it does not accurately capture the underlying relationships in the data. This can lead to underfitting, where the model performs poorly on both the training data and new data.
On the other hand, variance error arises when the model is too sensitive to the specific details of the training data, and as a result, it performs well on the training data but poorly on new data. This can lead to overfitting, where the model performs well on the training data but poorly on new data.
In the context of the naive Bayes algorithm, bias error arises when the algorithm makes too strong of an assumption about the independence of the features in the dataset. If the features are actually dependent on each other, the naive Bayes algorithm will make incorrect predictions because it is not accounting for these dependencies.
On the other hand, variance error arises when the algorithm is too sensitive to the specific details of the training data. This can happen if the dataset is small or if it contains a lot of noise. In this case, the naive Bayes algorithm may make predictions that are too heavily influenced by the specific details of the training data, and as a result, it may perform poorly on new data.
Overall, the bias-variance tradeoff is an important consideration when using the naive Bayes algorithm. The goal is to strike the right balance between bias and variance, to achieve the best performance on both the training data and new data. This may involve adjusting the smoothing parameter or the number of features used by the algorithm, or using other techniques to improve its performance.
Feature importance and interpretability
The naive Bayes algorithm is a simple and effective machine learning algorithm for classification tasks, but it has some limitations in terms of feature importance and interpretability.
One limitation of the naive Bayes algorithm is that it does not provide any information about the importance of the features in the dataset. This is because the algorithm assumes that all of the features are independent of each other, and therefore, it does not consider the relative importance of the features when making predictions. This means that it is not possible to use the naive Bayes algorithm to identify the most important features in the dataset, or to understand how the features are contributing to the predictions made by the algorithm.
Another limitation of the naive Bayes algorithm is that it is not very interpretable. This means that it is difficult to understand how the algorithm is making its predictions, or to explain the reasoning behind the predictions to others. This is because the algorithm is based on probabilities, and the probabilities are calculated using Bayes’ theorem, which is a complex mathematical concept. As a result, it can be difficult to understand how the algorithm is using the probabilities to make predictions, or to explain the predictions to others in a clear and intuitive way.
Overall, the naive Bayes algorithm is a simple and effective algorithm for classification tasks, but it has limitations in terms of feature importance and interpretability. If these limitations are a concern for your specific use case, you may want to consider using a different algorithm.
Imbalanced data
Imbalanced data is a common problem in machine learning, and it can affect the performance of the naive Bayes algorithm as well. Imbalanced data occurs when the classes in a dataset are not represented equally. For example, if a dataset contains 100 observations, and 95 of them belong to one class and 5 of them belong to another class, the dataset is said to be imbalanced.
The naive Bayes algorithm is sensitive to imbalanced data, because it relies on probabilities to make predictions. If the classes in the dataset are not represented equally, the probabilities calculated by the algorithm may be skewed, and as a result, the predictions made by the algorithm may not be accurate.
For example, suppose we have a dataset with two classes: “spam” and “not spam.” We want to train a naive Bayes classifier to predict the class of a new email, based on the words that appear in the email. If the dataset is imbalanced, with a much larger number of “not spam” emails than “spam” emails, the probabilities calculated by the algorithm may be skewed, and as a result, the classifier may have difficulty accurately identifying “spam” emails.
To address this problem, there are several strategies that can be used. One approach is to oversample the minority class, to make the classes in the dataset more balanced. This involves generating additional synthetic observations for the minority class, using techniques such as SMOTE (Synthetic Minority Oversampling Technique).
Another approach is to use a different evaluation metric, such as precision, recall, or F1 score, which are better suited for imbalanced datasets. These metrics take into account the imbalance in the classes, and they provide a more accurate measure of the performance of the classifier on imbalanced data.
Overall, imbalanced data can affect the performance of the naive Bayes algorithm, but there are strategies that can be used to address this problem. By oversampling the minority class or using a different evaluation metric, it is possible to improve the performance of the naive Bayes algorithm on imbalanced data.
Outliers
Outliers are observations in a dataset that are very different from the other observations. They can occur for a variety of reasons, such as errors in the data collection process, or the presence of rare or unusual events. Outliers can affect the performance of the naive Bayes algorithm, because they can have a disproportionate impact on the probabilities calculated by the algorithm.
To understand why outliers can affect the performance of the naive Bayes algorithm, consider an example where we have a dataset with two classes: “spam” and “not spam.” We want to train a naive Bayes classifier to predict the class of a new email, based on the words that appear in the email. If the dataset contains an outlier email that is very different from the other emails, it could have a significant impact on the probabilities calculated by the algorithm.
For example, suppose the dataset contains an outlier email that is very long and contains a large number of unique words. This email could cause the probabilities of many words to be much higher than they would be otherwise, because it would be counted as a separate observation for each of those words. As a result, the naive Bayes classifier could make incorrect predictions, because it would be basing its predictions on probabilities that are skewed by the outlier email.
To address this problem, there are several strategies that can be used. One approach is to identify and remove the outliers from the dataset, before training the naive Bayes classifier. This can be done using a variety of outlier detection algorithms, which use statistical or mathematical techniques to identify observations that are very different from the other observations in the dataset.
Another approach is to use a different algorithm that is less sensitive to outliers. For example, some algorithms are more robust to outliers, because they use a different approach to calculate probabilities or make predictions. These algorithms may be less affected by outliers, and as a result, they may produce more accurate predictions.
Overall, outliers can affect the performance of the naive Bayes algorithm, but there are strategies that can be used to address this problem. By identifying and removing the outliers, or using a different algorithm that is less sensitive to outliers, it is possible to improve the performance of the naive Bayes algorithm.
Missing values
Missing values are a common problem in machine learning, and they can affect the performance of the naive Bayes algorithm as well. Missing values occur when a dataset contains observations that are incomplete, and as a result, some of the values for the features of those observations are missing. This can happen for a variety of reasons, such as errors in the data collection process, or the presence of rare or unusual events.
The naive Bayes algorithm is sensitive to missing values, because it relies on probabilities to make predictions. If a dataset contains missing values, the probabilities calculated by the algorithm may be incorrect, and as a result, the predictions made by the algorithm may not be accurate.
To understand why missing values can affect the performance of the naive Bayes algorithm, consider an example where we have a dataset with two classes: “spam” and “not spam.” We want to train a naive Bayes classifier to predict the class of a new email, based on the words that appear in the email. If the dataset contains missing values for some of the words in the emails, the probabilities calculated by the algorithm may be incorrect, and as a result, the classifier may make incorrect predictions.
To address this problem, there are several strategies that can be used. One approach is to impute the missing values, using a variety of imputation algorithms. These algorithms use statistical or mathematical techniques to estimate the missing values based on the other observations in the dataset.
Another approach is to use a different algorithm that is less sensitive to missing values. For example, some algorithms are more robust to missing values, because they use a different approach to calculate probabilities or make predictions. These algorithms may be less affected by missing values, and as a result, they may produce more accurate predictions.
Overall, missing values can affect the performance of the naive Bayes algorithm, but there are strategies that can be used to address this problem. By imputing the missing values, or using a different algorithm that is less sensitive to missing values, it is possible to improve the performance of the naive Bayes algorithm.
Handling Numerical features (Gaussian NB)
The naive Bayes algorithm is a simple and effective machine learning algorithm for classification tasks, but it has some limitations when it comes to handling numerical features. The algorithm assumes that the features in the dataset are independent and follow a specific probability distribution (usually a Gaussian distribution), and as a result, it is not well-suited to datasets with numerical features that do not meet these assumptions.
To address this problem, there is a variant of the naive Bayes algorithm called Gaussian naive Bayes, which is specifically designed to handle numerical features. This variant assumes that the numerical features in the dataset are normally distributed, and it uses the Gaussian distribution to calculate probabilities and make predictions.
To understand how Gaussian naive Bayes works, consider an example where we have a dataset with two classes: “spam” and “not spam.” We want to train a Gaussian naive Bayes classifier to predict the class of a new email, based on the length of the email and the number of unique words that appear in the email. In this case, the length and number of unique words are numerical features, and they need to be handled differently from the other features in the dataset.
To do this, the Gaussian naive Bayes classifier first calculates the mean and standard deviation of the length and number of unique words for each class (i.e., “spam” and “not spam”). Then, for each new email, it calculates the probability that the email belongs to each class, using the Gaussian distribution. This involves plugging the values for the length and number of unique words into the Gaussian formula, along with the calculated mean and standard deviation for each class. Finally, the classifier compares the probabilities of the email belonging to each class, and chooses the class with the highest probability as the predicted class for the email.
In summary, Gaussian naive Bayes is a variant of the naive Bayes algorithm that is specifically designed to handle numerical features. It assumes that the numerical features in the dataset are normally distributed, and it uses the Gaussian distribution to calculate probabilities and make predictions. This allows the Gaussian naive Bayes algorithm to make more accurate predictions on datasets with numerical features. By using the Gaussian distribution to calculate probabilities, the algorithm is able to take into account the specific characteristics of the numerical features in the dataset, and make more accurate predictions. This can be especially useful in cases where the numerical features are not independent, or do not follow a uniform distribution, as is often the case with real-world data.
Multiclass classification
Multiclass classification is a machine learning task that involves predicting a label from more than two classes. For example, in a dataset with three classes: “dog,” “cat,” and “bird,” a multiclass classifier would be tasked with predicting which of these three classes a new observation belongs to.
The naive Bayes algorithm is well-suited to multiclass classification tasks, because it can easily handle multiple classes. This is because the algorithm is based on Bayes’ theorem, which is a mathematical formula that allows the algorithm to calculate the probability of an observation belonging to each of the classes in the dataset.
To understand how the naive Bayes algorithm can be used for multiclass classification, consider an example where we have a dataset with three classes: “dog,” “cat,” and “bird.” We want to train a naive Bayes classifier to predict the class of a new animal, based on the features of the animal (such as its size, shape, and color).
To do this, the naive Bayes classifier first calculates the probability of each class in the dataset, using the training data. Then, for each new animal, it calculates the probability of the animal belonging to each class, based on the features of the animal. Finally, the classifier compares the probabilities of the animal belonging to each class, and chooses the class with the highest probability as the predicted class for the animal.
In summary, the naive Bayes algorithm is well-suited to multiclass classification tasks, because it can easily handle multiple classes. By using Bayes’ theorem to calculate the probabilities of an observation belonging to each class, the algorithm is able to make accurate predictions on multiclass classification tasks.
Similarity or Distance matrix
The similarity or distance matrix is a tool used in some machine learning algorithms, including the naive Bayes algorithm, to measure the similarity or distance between different observations in a dataset. The similarity or distance matrix is a mathematical representation of the relationships between the observations in the dataset, and it can be used to improve the performance of the algorithm by providing a more accurate representation of the data.
To understand how the similarity or distance matrix is used in the naive Bayes algorithm, consider an example where we have a dataset with two classes: “spam” and “not spam.” We want to train a naive Bayes classifier to predict the class of a new email, based on the words that appear in the email. In this case, the similarity or distance matrix can be used to measure the similarity or distance between different emails in the dataset, based on the words that appear in the emails.
To create the similarity or distance matrix, the algorithm first calculates the probabilities of each word appearing in each class (i.e., “spam” and “not spam”). This is done in the same way as for binary classification, by counting the number of times each word appears in each class, and dividing by the total number of words in each class. Then, for each pair of emails in the dataset, the algorithm calculates the similarity or distance between the emails, using the probabilities of the words that appear in the emails. This involves multiplying the probabilities of each word appearing in each class, to get the overall similarity or distance between the emails. Finally, the algorithm uses the similarity or distance matrix to improve the performance of the naive Bayes classifier, by providing a more accurate representation of the relationships between the emails in the dataset.
In summary, the similarity or distance matrix is a tool used in the naive Bayes algorithm to measure the similarity or distance between different observations in a dataset. The matrix is created by calculating the probabilities of each word appearing in each class, and using those probabilities to calculate the overall similarity or distance between the observations in the dataset. The matrix is then used to improve the performance of the naive Bayes classifier, by providing a more accurate representation of the relationships between the observations in the dataset. This can help the classifier make more accurate predictions, by taking into account the specific similarities or distances between the observations in the dataset.
Large dimensionality
The naive Bayes algorithm is a simple and effective machine learning algorithm for classification tasks, but it has some limitations when it comes to handling large dimensionality. Large dimensionality occurs when a dataset has a large number of features (also known as dimensions), which can make the algorithm less effective and more difficult to use.
One limitation of the naive Bayes algorithm when it comes to large dimensionality is that it becomes computationally expensive to calculate probabilities for all of the features in the dataset. This is because the algorithm relies on probabilities to make predictions, and it calculates these probabilities by multiplying the probabilities of each feature (i.e., dimension) in the dataset. For large datasets with many features, this can be very time-consuming and require a lot of computational resources.
Another limitation of the naive Bayes algorithm when it comes to large dimensionality is that it can suffer from the curse of dimensionality. The curse of dimensionality occurs when the number of features in the dataset is much larger than the number of observations, and as a result, the data becomes sparse and difficult to model accurately. This can cause the algorithm to make less accurate predictions, because it is unable to capture the underlying patterns in the data.
To address these problems, there are several strategies that can be used. One approach is to reduce the dimensionality of the dataset, using a variety of dimensionality reduction techniques. These techniques remove redundant or irrelevant features from the dataset, to reduce the number of dimensions and make the data more manageable.
Another approach is to use a different algorithm that is less sensitive to large dimensionality. For example, some algorithms are more robust to large dimensionality, because they use a different approach to calculate probabilities or make predictions. These algorithms may be less affected by the curse of dimensionality, and as a result, they may produce more accurate predictions on large datasets with many features.
Overall, large dimensionality can affect the performance of the naive Bayes algorithm, but there are strategies that can be used to address this problem. By reducing the dimensionality of the dataset or using a different algorithm, it is possible to improve the performance of the naive Bayes algorithm on large datasets with many features.
Best and worst cases
The naive Bayes algorithm is a simple and effective machine learning algorithm for classification tasks, but like any algorithm, it has its strengths and weaknesses, and it performs better in some cases than others. In general, the best and worst cases for the naive Bayes algorithm depend on a variety of factors, including the characteristics of the dataset and the specific goals of the classification task.
One of the best cases for the naive Bayes algorithm is when the dataset is well-behaved and follows the assumptions of the algorithm. The naive Bayes algorithm assumes that the features in the dataset are independent and follow a specific probability distribution (usually a Gaussian distribution), and when the dataset meets these assumptions, the algorithm can make highly accurate predictions. For example, if the dataset contains numerical features that are normally distributed and the classes in the dataset are well-separated, the naive Bayes algorithm can perform very well.
Another best case for the naive Bayes algorithm is when the dataset is large and contains a sufficient number of observations for each class. The algorithm relies on probabilities to make predictions, and it calculates these probabilities by counting the number of times each feature appears in each class. Therefore, the more observations the algorithm has to work with, the more accurate the probabilities will be, and the more accurate the predictions will be.
On the other hand, one of the worst cases for the naive Bayes algorithm is when the dataset does not follow the assumptions of the algorithm. If the features in the dataset are not independent, or if they do not follow a specific probability distribution, the algorithm can make inaccurate predictions. For example, if the dataset contains categorical features that are highly correlated, the naive Bayes algorithm may struggle to make accurate predictions.
Another worst case for the naive Bayes algorithm is when the dataset is small and contains a limited number of observations for each class. In this case, the probabilities calculated by the algorithm may be inaccurate, because they are based on a small number of observations. This can cause the algorithm to make incorrect predictions, because it is unable to capture the underlying patterns in the data.
Overall, the best and worst cases for the naive Bayes algorithm depend on the characteristics of the dataset and the specific goals of the classification task. In general, the algorithm performs well when the dataset is well-behaved and follows the assumptions of the algorithm, and when the dataset is large and contains a sufficient number of observations for each class. On the other hand, the algorithm can perform poorly when the dataset does not follow the assumptions of the algorithm, or when the dataset is small and contains a limited number of observations for each class. In these cases, the naive Bayes algorithm may struggle to make accurate predictions, and other algorithms may be more suitable for the classification task.
